본 글은 모두를 위한 R 데이터 분석 입문 책을 공부하면서 정리·요약한 내용입니다.
저자 : 오세종
출판 : 한빛아카데미
1. - 4 -
2. - 4 - 종속변수, 독립변수는 상관분석과 아무런 관계가 없다. -> 회귀분석과 관계가 있음
3. - 4 - 상관관계랑 분산은 관계가 없다.
복습
단일변수 - 팩터형(질적), 연속형(양적)
팩터형 : 도수분포표, 막대그래프, 원 그래프
연속형 : 기술통계, 히스토그램, 상자그림
다중변수 - 산점도, 상관분석
산점도 : plot(), pairs(), ~ 사용시 y축 ~ x축
상관분석 : 한 변수가 변화함에 따라 다른 변수가 어떻게 변화하는지와 같은 변화의 강도와 방향
피어슨 상관계수 : 등간(구간)척도, 비율척도(연속형)로 측정된 두 변수들의 상관관계를 측정
-1 ≤ r ≤ 1
r > 0 : 양의 상관관계(x가 증가하면 y도 증가)
r < 0 : 음의 상관관계(x가 증가하면 y는 감소)
r이 1이나 –1에 가까울수록 x, y의 상관성이 높음
스피어만 상관계수 : 서열척도인 두 변수들이 상관관계를 측정
# 코드 복습
? mtcars
str(mtcars)
head(mtcars)
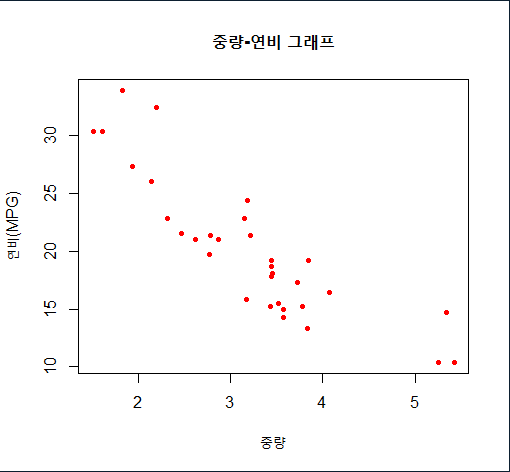
wt <- mtcars$wt # 중량 자료
mpg <- mtcars$mpg # 연비 자료
plot(wt, mpg, # x축, y축
main="중량-연비 그래프", # 제목
xlab="중량", # x축 레이블
ylab="연비(MPG)", # y축 레이블
col="red", # point의 color
pch=20) # point의 종류
cor(iris[,1:4]) # 4개 변수 간 상관성 분석

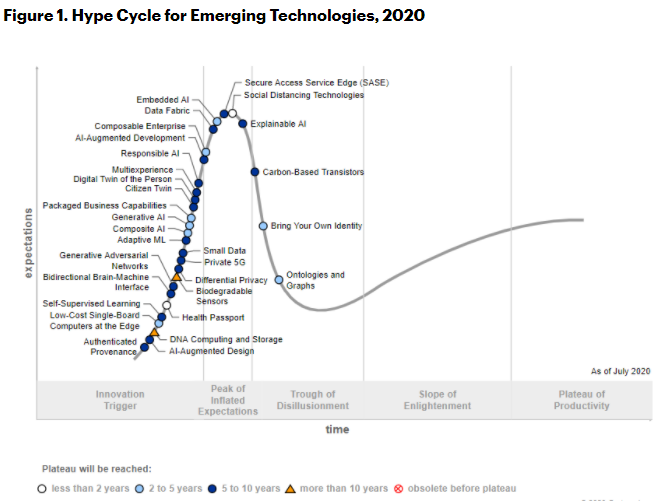
Hype Cycle for Emerging Technologies
하이프 사이클은 기술의 성숙도를 표현하기 위한 시각적 도구
과대광고 주기라고도 함
미국의 정보 기술 연구 및 자문 회사인 가트너에서 개발함
<2020 Hype Cycle for Emerging Technologies> : https://www.gartner.com/en/newsroom/press-releases/2020-08-18-gartner-identifies-five-emerging-trends-that-will-drive-technology-innovation-for-the-next-decade
if - else문
x <- 4
if (x %% 2 == 0){
print('x는 짝수')
} else{
print('x는 홀수')
}
다중 if - else문
x <- 0
if(x > 0){
print('x는 양수')
} else if(x < 0){
print('x는 음수')
} else{
print('x는 0')
}
논리 연산자
a <- 10
b <- 20
if (a>5 & b>5){
print(a + b)
}
if (a>5 | b>30){
print(a * b)
}
for문 (형식이 다른언어와 조금 다르다.)
for(i in 2:9){
for(j in 1:9){
cat(i, '*', j, '=', i*j, '\n')
}
cat('\n')
}
연습문제
1) 1~100 사이의 정수 중 3의 배수들의 합과 개수를 구하시오.
sum <- 0 # 배수들의 합
cnt<- 0 # 배수들의 개수
for(i in 1:100) {
if (i%%3==0) {
sum <- sum + i
cnt <- cnt + 1
}
}
sum
cnt
2) 101~200 사이의 숫자 중 3과 4의 공배수를 출력하시오.
for(i in 101:200){
if(i%%3==0 & i%%4==0){
cat(i, " ")
}
}
3) 24의 약수를 출력하시오.
for(i in 1:24){
if(24%%i==0){
cat(i, " ")
}
}
Boston Housing 데이터 셋
미국 보스턴 지역의 주택 가격 정보와 주택 가격에 영향을 미치는 여러 요소들에 대한 정보를 담고 있음
1단계 : 분석 대상 데이터 셋 준비
install.packages('mlbench') # 패키지 설치
library(mlbench) # 패키지 활성화
? BostonHousing # 데이터 셋 설명
data(BostonHousing) # 패키지에서 데이터 셋 로딩
BostonHousing # 데이터 셋 출력
str(BostonHousing) # 데이터 셋 요약
myds <- BostonHousing[, c("crim", "rm", "dis", "tax", "medv")] # 사용할 5개의 변수만 추출
2단계 : grp 변수 추가
# grp는 주택 가격을 상(H), 중(M), 하(L)로 분류한 것으로 25.0 이상이면 상(H), 17.0 이하이면 하(L), 나머지를 중(M)으로 분류
grp <- c() # 빈 벡터 생성
for(i in 1:nrow(myds)){
if(myds$medv[i] >= 25.0){ # medv는 자가주택의 중간 값 단위는 1000$
grp[i] <- "H"
} else if(myds$medv[i] <= 17.0){
grp[i] <- "L"
} else{
grp[i] <- "M"
}
}
grp <- factor(grp) # 문자 벡터를 팩터 타입으로 변경
grp <- factor(grp, levels=c("H", "M", "L")) # 순서 재배열 (원래는 "H", "L", "M")
myds <- data.frame(myds, grp) # myds에 grp 열 추가
3단계 : 데이터셋의 형태와 기본적인 내용 파악
# table() 함수를 통해 도수분포표를 작성
str(myds)
head(myds)
for.graph <- table(myds$grp)
barplot(for.graph) # 막대 그래프 작성
pie(for.graph) # 원 그래프 작성
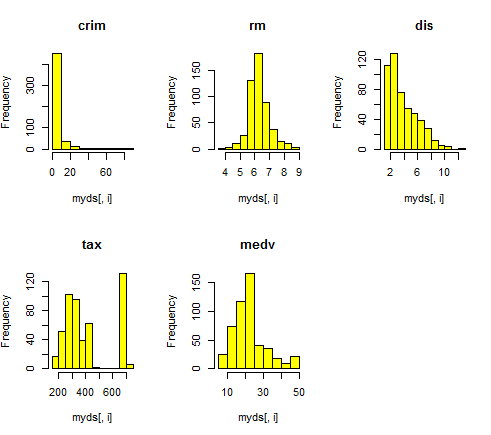
4단계 : 히스토그램에 의한 관측값의 분포 확인
par(mfrow=c(2,3)) # 2x3 가상화면 분할
for(i in 1:5){
hist(myds[,i], main=colnames(myds)[i], col="yellow") # 열 제목 변경
}
par(mfrow=c(1,1)) # 가상화면 분할 해제
분석 결과 :
rm(주택 1가구당 방의 개수), medv(주택 가격) 변수만 종 모양의 정규분포에 가깝고, crim(지역의 1인당 범죄율), dis(직업 센터까지 거리)는 관측값들이 한쪽으로 쏠려서 분포
tax(재산세율)는 중간에 관측값이 없는 빈 구간이 존재하는 특징
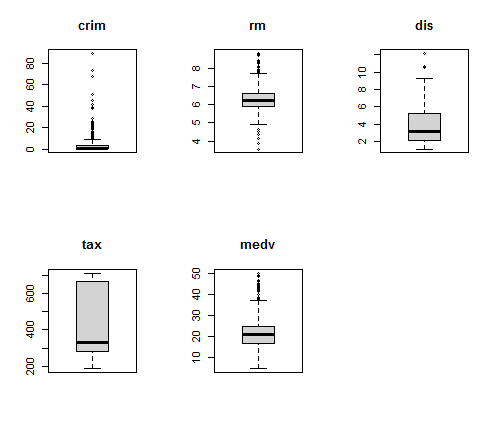
5단계 : 상자그림에 의한 관측값의 분포 확인
# 그룹 정보(grp)를 제외한 5개 변수에 대해 상자그림 작성
par(mfrow=c(2,3))
for(i in 1:5){
boxplot(myds[,i], main=colnames(myds)[i])
}
par(mfrow=c(1,1))
분석 결과 :
1인당 범죄율(crim)은 관측값들이 좁은 지역에 밀집되어 있음(관측값들의 편차가 매우 작음)
재산세율(tax)은 넓게 퍼져 있는 것(관측값들의 편차가 비교적 크다)을 확인
6단계 : 그룹별 관측값 분포의 확인
# 그룹 정보를 이용하여 각 변수별로 그룹별 분포를 확인
boxplot(myds$crim~myds$grp, main="1인당 범죄율")
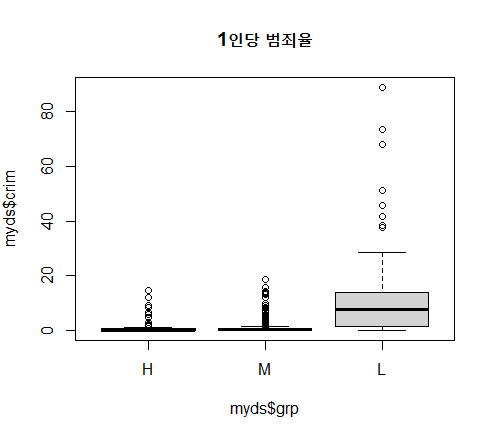
분석 결과 :
주택 가격이 높은 지역이나 중간 지역의 범죄율은 낮고, 주택 가격이 낮은 지역의 범죄율이 높게 나타남
boxplot(myds$rm~myds$grp, main="방의 개수")
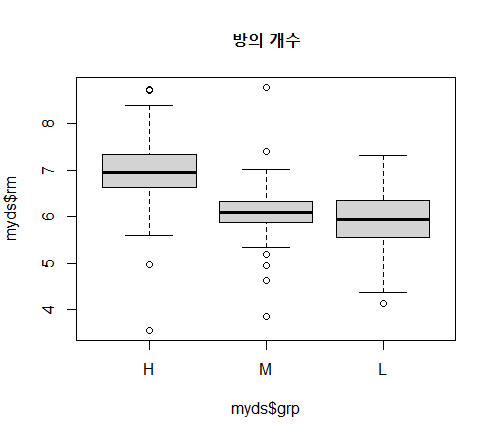
분석 결과 :
주택 가격이 높으면 방의 개수도 많다는 것을 알 수 있음
주택 가격이 중간인 지역과 하위인 지역의 방의 개수 중간값은 큰 차이가 나지 않음
중간 그룹의 방의 개수가 5.2~6.8 사이로 비교적 균일한 반면 하위그룹의 방의 개수는 4.5~7.2 사이로 넓게 퍼져 있는 것을 알 수 있음
7단계 : 다중 산점도를 통한 변수 간 상관 관계의 확인
pairs(myds[,-6])
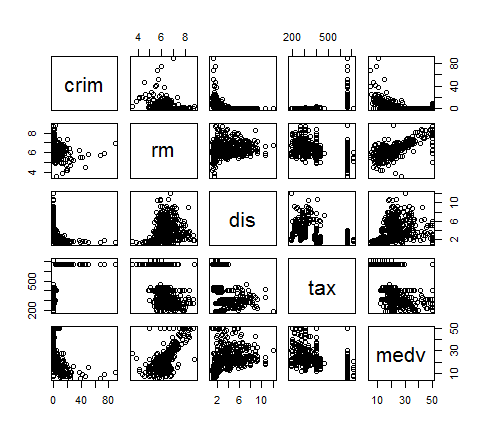
분석 결과 :
medv(주택 가격)과 양의 상관성이 있는 변수는 rm(가구당 방의 개수)
crim(1인당 범죄율)은 주택 가격과 음의 상관성이 있는 것으로 보임
8단계 : 그룹 정보를 포함한 변수 간 상관 관계의 확인
point <- as.integer(myds$grp) # 점의 모양 지정
color <- c("red", "green", "blue") # 점의 색 지정
pairs(myds[,-6], pch=point, col=color[point])
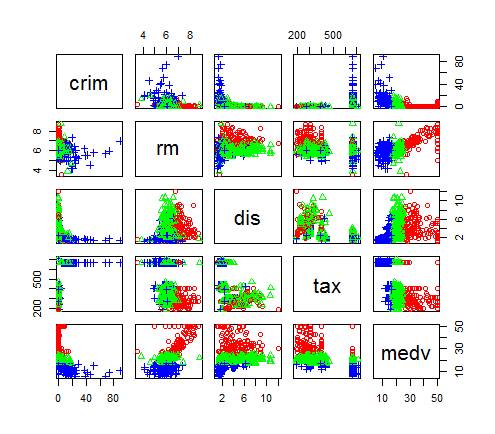
분석 결과 :
(crim-medv), (rm-medv), (dis-medv), (tax-medv) 산점도에서 그룹별로 분포 위치가 뚜렷하게 구분
주택 가격 중간 그룹(녹색점들)은 상위 그룹(빨간색), 하위 그룹(파란색)에 비해 주택 가격의 변동폭이 좁음
9단계 : 변수 간 상관계수의 확인
cor(myds[,-6])

분석결과 :
medv(주택가격)를 기준으로 보았을 때 상관계수가 가장 높은 것은 rm(가구당 방의 개수)으로 0.6953599
산점도상에서 음의 상관성이 높은 것으로 보였던 crim(1인당 범죄율)은 상관계수가 -0.3883046으로, 실제로는 상관도가 높지 않음
연습문제
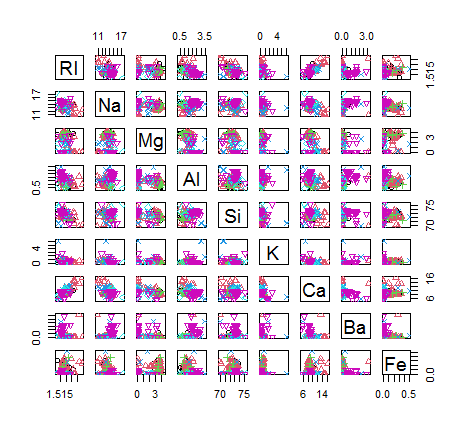
1) Glass 데이터셋을 myds에 저장하시오.
myds <- Glass
2) myds에서 Type을 제외한 변수들 간의 분포를 산점도를 통해 보이시오.
pairs(myds[,-10])

3) myds에서 Type을 제외한 변수들 간의 분포를 상관계수를 통해 확인하시오.
cor(myds[,-10])

4) myds에서 Type을 제외한 변수들 간의 분포를 산점도를 통해 보이되 Type을 그룹으로 하여 그룹별로 점의 색을 달리하시오.
point <- as.integer(myds$Type)
pairs(myds[,-10], pch=point, col=myds$Type) # col = 기본색상
데이터 전처리(Data Preprocessing)
특정 분석에 적합하게 데이터를 가공하는 작업을 의미
초기 데이터에는 정상 범위를 넘어서는 값이나 오류 데이터가 포함되어 있는 경우도 있기 때문에 이를 처리하지 않으면 통계 결과가 왜곡될 수도 있음
결측값(missing value)
데이터를 수집하고 저장하는 과정에서 고의 또는 실수로 저장할 값을 얻지 못하는 경우 발생
결측값의 처리 방법
- 결측값 제외하고 분석
- 적당한 값으로 치환 후 분석
결측값의 특성과 존재 여부 확인
z <- c(1, 2, 3, NA, 5, NA, 8) # 결측값이 포함된 벡터 z
sum(z) # 정상 계산이 안됨 (NA)
is.na(z) # NA 여부 확인 (FALSE FALSE FALSE TRUE FALSE TRUE FALSE)
sum(is.na(z)) # NA의 개수 확인 (2)
sum(z, na.rm=TRUE) # NA를 제외하고 합계를 계산 (19)
'데이터 분석 > R' 카테고리의 다른 글
| 데이터 분석[R] - 7차시 (0) | 2021.07.05 |
|---|---|
| 데이터 분석[R] - 6차시 (0) | 2021.07.02 |
| 데이터분석[R] - 4차시 (0) | 2021.06.30 |
| 데이터 분석[R] - 3차시 (0) | 2021.06.29 |
| 데이터분석 [R] - 2차시 (0) | 2021.06.28 |



