본 글은 모두를 위한 R 데이터 분석 입문 책을 공부하면서 정리·요약한 내용입니다.
저자 : 오세종
출판 : 한빛아카데미
다음 중 R의 데이터 구조 중 벡터에 대한 설명으로 적절한 것은? - 2 -
① 벡터는 행과 열을 갖는 m X n 형태의 직사각형에 데이터를 나열한 데이터구조이다.
② 벡터는 하나의 스칼라 값 또는 하나 이상의 스칼라 원소들을 갖는 단순한형태의 집합이다.
③ 벡터는 행렬과 유사한 2차원 목록 데이터 구조이다.
④ 벡터는 숫자로만 구성되어야 한다.
다음 중 결과가 다른 R 코드는? - 2 -
① a<-seq(1,10,1)
② b<-c(1,10)
③ c<-1:10
④ d<-seq(10,100,10)/10
R에서 y=c(1,2,3,NA)일때 3*y의 실행 결과는? - 4 -
① 에러가 발생하고 결과가 출력되지 않는다.
② 3 6 9 0
③ 3 6 9 3
④ 3 6 9 NA
Gapminder
갭마인더(Gapminder)는 스웨덴의 비영리 통계분석 서비스로 다양한 통계자료들을 제공한다.
런던 지하철의 차량과 승강장 틈새를 조심하라는 경고문(Mind the gap)에서 가져온 이름은, 생각과 실제의 차이를 극복하자는 철학을 담고 있다.
https://www.gapminder.org/tools/#$chart-type=linechart&url=v1
위 URL로 들어가면 아래 사진과 같이 GDP의 통계를 확인할 수 있다.
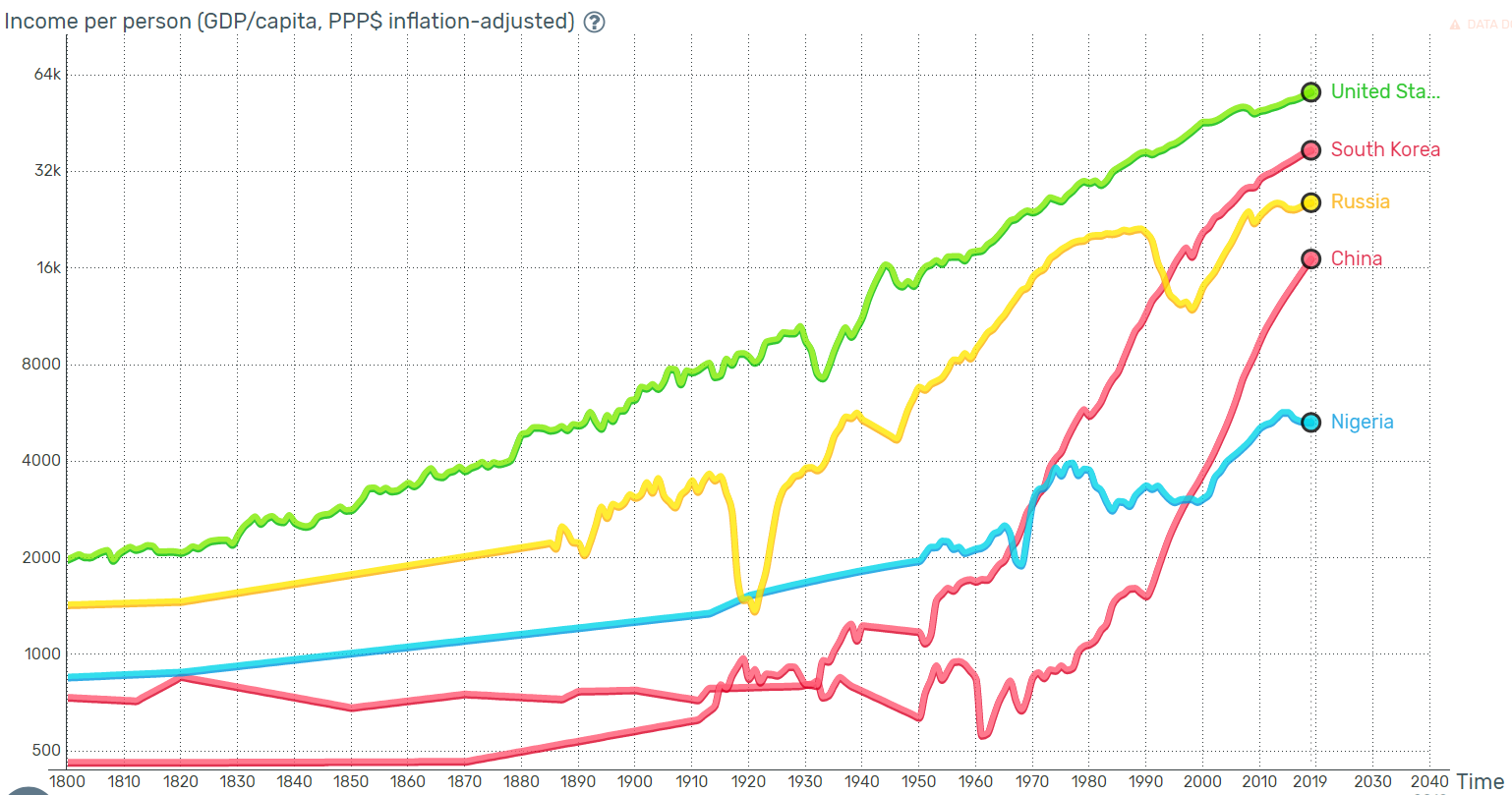
자료의 종류
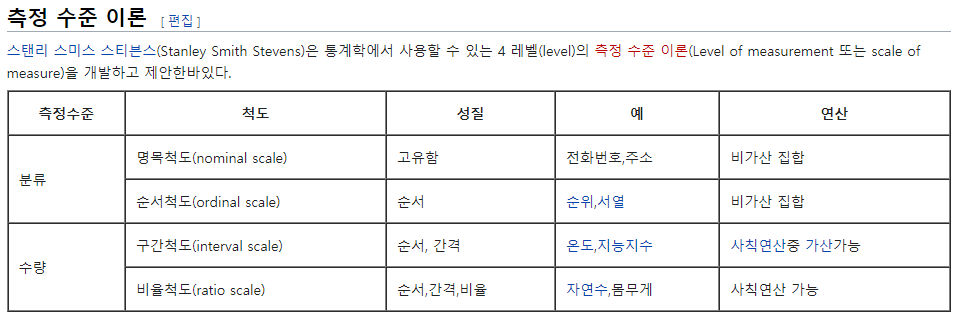
출처 : 위키피디아
단일 변수와 다중 변수
통계학에서의 변수는 우리가 연구, 조사, 관찰하고 싶은 대상의 특성을 의미
단일변수 자료(univariate data) : 하나의 변수로만 구성된 자료, ‘일변량 자료’라고도 부름
다중변수 자료(multivariate data) : 두 개 이상의 변수로 구성된 자료, 다변량 자료라고 부름 (두 개의 변수로 구성된 자료 -> 이변량 자료)
단일 변수 범주형 자료의 탐색
단일 변수 범주형 자료(또는 일변량 질적 자료): 특성이 하나이면서 자료의 특성이 범주형인 자료
범주형 자료에 대해서 할 수 있는 기본적인 작업은 자료에 포함된 관측값들의 종류별로 개수를 세는 것
개수를 세면 종류별 비율을 알 수 있음
막대그래프나 원그래프의 작성이 가능
도수분포표의 작성 (학생들이 선호하는 계절에 대한 단일 변수 범주형 자료)
favorite <- c("WINTER", "SUMMER", "SPRING", "SUMMER", "SUMMER", "FALL",
"FALL", "SUMMER", "SPRING", "SPRING")
favorite # favorite의 내용 출력

table(favorite) # 도수분포표 계산
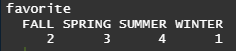
table(favorite)/length(favorite) # 비율 출력
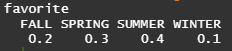
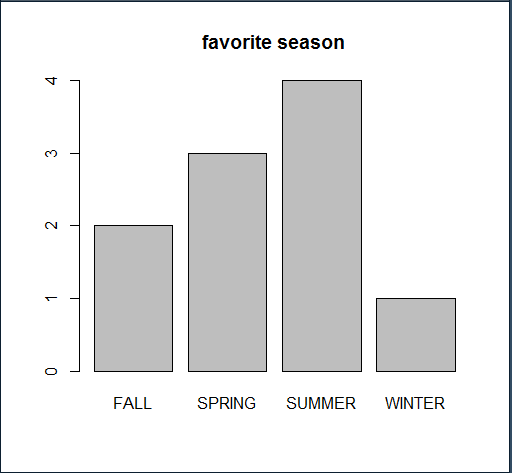
막대그래프의 작성 (학생들이 선호하는 계절에 대한 단일 변수 범주형 자료)
tf <- table(favorite)
tf
barplot(tf, main='favorite season')
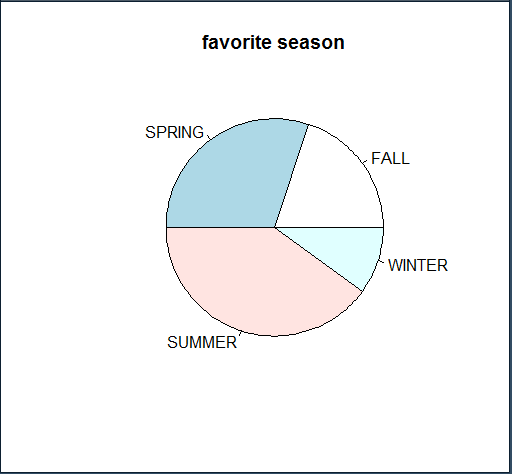
원 그래프의 작성 (학생들이 선호하는 계절에 대한 단일 변수 범주형 자료)
ds <- table(favorite)
ds
pie(ds, main='favorite season')
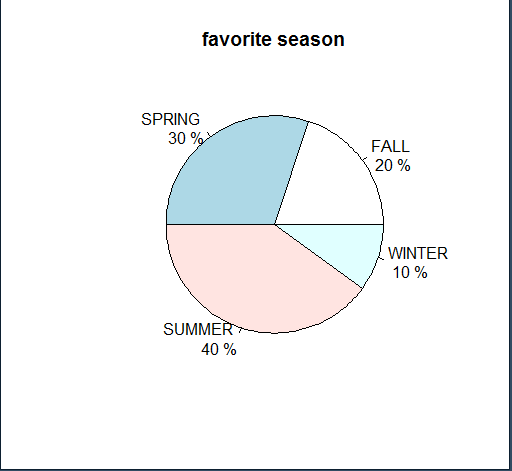
원 그래프의 작성 (퍼센트 표시) (학생들이 선호하는 계절에 대한 단일 변수 범주형 자료)
pct <- ds / sum(ds) * 100
label <- paste(names(ds), "\n", pct, "%")
pie(ds, main='favorite season', labels=label)
단일 변수 범주형 자료 예제
1) 네이버 밴드에서 글쓰기 -> 투표
가장 즐겨듣는 음악 장르에 대한 투표 진행
2) 투표 결과로 벡터 만들기
genre <- c('발라드', '발라드', '발라드', '발라드', '발라드',
'기타', '기타', '기타', '기타',
'힙합', '힙합', '힙합',
'댄스', '댄스',
'K-POP')
3) 도수분포표
table(genre)
4) 막대 그래프 그리기
ds <- table(genre)
barplot(ds, main='favorite music jenre') # ds는 벡터 X, 테이블 O
5) 원 그래프 그리기
ds <- table(genre)
pie(ds, main='favorite music jenre')
6) 원 그래프 그리기 (퍼센트 표시)
pct <- round(ds / sum(ds) * 100, 2) # round()는 소수 두번째 자리까지만 출력
label <- paste(names(ds), "\n", pct, "%")
pie(ds, main='favorite music jenre', labels=label)
숫자로 된 범주형 자료

favorite.color <- c(2, 3, 2, 1, 1, 2, 2, 1, 3, 2, 1, 3, 2, 1, 2)
ds <- table(favorite.color)
ds
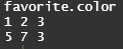
barplot(ds, main='favorite color')
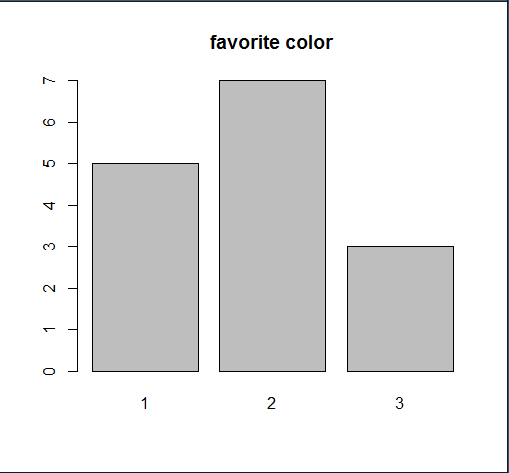
colors <- c('green', 'red', 'blue')
names(ds) <- colors # name 1, 2, 3을 green, red, blue로 변경
ds
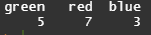
barplot(ds, ,main='favorite color', col=colors) # 색 지정 막대 그래프
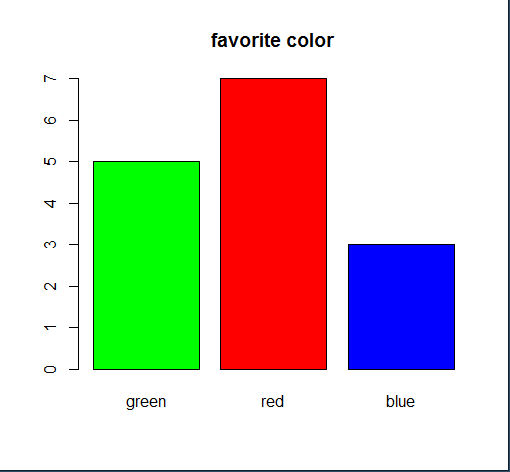
pie(ds, main='favorite color', col=colors) # 색 지정 막대 원 그래프
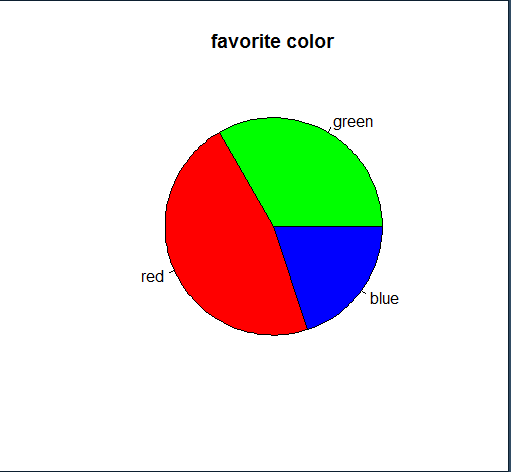
평균과 중앙값
연속형 자료(양적 자료)는 관측값들이 크기를 가지기 때문에 범주형 자료(질적 자료)에 비해 다양한 분석 방법이 존재
평균 -> 이상값(특이값)이 있는 경우 크게 영향 받음
중앙값 : 자료의 값들을 크기순으로 일렬로 줄 세웠을 때, 가장 중앙에 위치하는 값 -> 이상값의 영향을 거의 받지 않음
# 1, 2, 3, 4, 5 -> 중앙값 : 3
# 1, 2, 3, 4, 5, 6 -> 중앙값 : 3.5
weight <- c(60, 62, 64, 65, 68, 69)
weight.heavy <- c(weight, 120)
weight
weight.heavy
mean(weight) # 평균 64.66667
mean(weight.heavy) # 평균 72.57143
median(weight) # 중앙값 64.5
median(weight.heavy) # 중앙값 65
사분위수
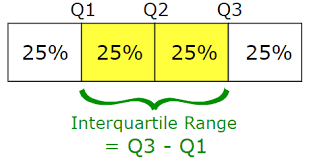
주어진 자료에 있는 값들을 크기순으로 나열했을 때 이것을 4등분하는 지점에 있는 값들을 의미
자료에 있는 값들을 4등분하면 등분점이 3개 생기는데, 앞에서부터 ‘제1사분위수(Q1)’, ‘제2사분위수(Q2)’, ‘제3사분위수(Q3)’라고 부르며, 제2사분위수(Q2)는 중앙값과 동일
전체 자료를 4개로 나누었기 때문에 4개의 구간에는 각각 25%의 자료가 존재
mydata <- c(60, 62, 64, 65, 68, 69, 120)
quantile(mydata) # 사분위수

summary(mydata) # 요약

산포
산포(distribution)란 주어진 자료에 있는 값들이 퍼져 있는 정도(흩어져 있는 정도)
다른 말로는 평균으로부터 얼마나 떨어져 있는가? 라는 의미
산포는 수학시간에 배운 분산(variance)과 표준편차(standard deviation)를 가지고 파악
자료의 분산과 표준편차가 작다는 의미는 자료의 관측값들이 평균값 부근에 모여 있다는 뜻
mydata <- c(60, 62, 64, 65, 68, 69, 120)
var(mydata) # 분산 447.2857
sd(mydata) # 표준편차 21.14913 => 평균 72.57143를 기준으로 ± 표준편차 21.14913로 데이터가 산포함.
range(mydata) # 값의 범위 (최소값과 최대값) 60 120
diff(range(mydata)) # 최댓값, 최솟값의 차이 60
히스토그램
히스토그램(histogram)은 표로 되어 있는 도수 분포를 정보 그림으로 나타낸 것
외관상 막대그래프와 비슷한 그래프로, 연속형 자료의 분포를 시각화할 때 사용
막대그래프를 그리려면 값의 종류별로 개수를 셀 수 이어야 하는데, 키와 몸무게 등의 자료는 값의 종류라는 개념이 없어서 종류별로 개수를 셀 수 없음
대신에 연속형 자료에서는 구간을 나누고 구간에 속하는 값들의 개수를 세는 방법을 사용
str(cars)
dist <- cars[, 2] # 자동차 제동거리
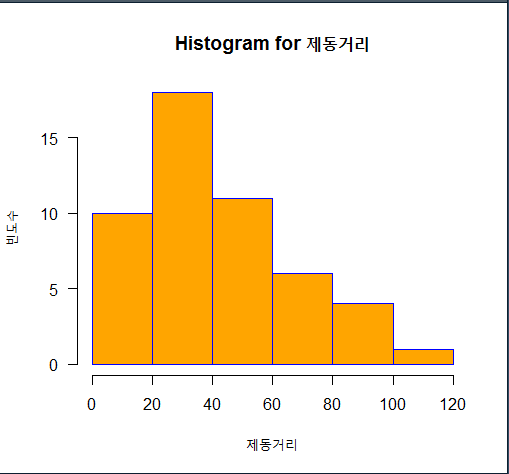
hist(dist, # 자료(data)
main="Histogram for 제동거리", # 제목
xlab="제동거리", # x축 레이블
ylab="빈도수", # y축 레이블
border="blue", # 막대 테두리색
col="orange", # 막대 색
las=1, # x축 글씨 방향(0~3)
breaks=5) # 막대 개수 조절
상자 수염 그림
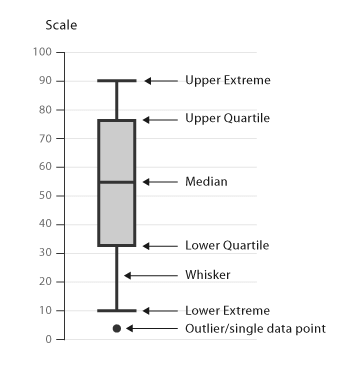
상자그림(box plot)은 상자 수염 그림(box and whisker plot)으로도 부르며, 사분위수를 시각화하여 그래프 형태로 나타낸 것
이 그래프는 가공하지 않은 자료 그대로를 이용하여 그린 것이 아니라, 자료로부터 얻어낸 통계량인 5가지 요약 수치(다섯 숫자 요약 five-number summary)를 가지고 그린다.
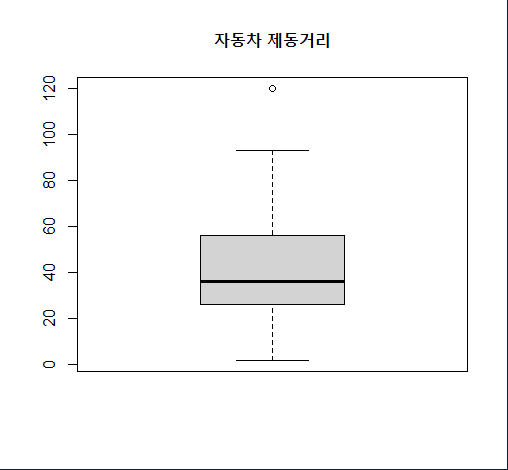
str(cars)
dist <- cars[, 2] # 자동차 제동거리(단위: 피트)
boxplot(dist, main="자동차 제동거리")
boxplot.stats(dist)
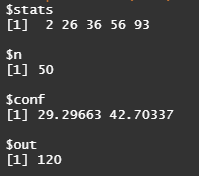
$stats : 최소값, Q1, Q2, Q3, 최대값
$n : 데이터 개수
$conf : 신뢰구간
$out : 특이값
학생 A의 과목별 성적이 다음과 같을 때 각 문제를 해결하시오.
1) 위 데이터를 score 벡터에 저장하시오(과목명은 데이터 이름으로 저장).
score <- c(90, 85, 73, 80, 85, 65, 78, 50, 68, 96)
names(score) <- c('KOR', 'ENG', 'ATH', 'HIST', 'SOC', 'MUSIC', 'BIO',
'EARTH', 'PHY', 'ART')
2) score 벡터의 내용을 출력하시오.
score
3) 전체 성적의 평균과 중앙값을 각각 구하시오.
mean(score)
median(score)
4) 전체 성적의 표준편차를 출력하시오.
sd(score)
5) 가장 성적이 높은 과목의 이름을 출력하시오. names(score[score==max(score)])
names(score[score == max(score)])
6) 성적에 대한 상자그림을 작성하시오.
boxplot(score)
7) 다음 조건을 만족하는 위 성적에 대한 히스토그램을 작성하시오.(그래프 제목: 학생 성적, 막대의 색: 보라색)
hist(score, main='학생성적', col='purple')
'데이터 분석 > R' 카테고리의 다른 글
| 데이터 분석[R] - 6차시 (0) | 2021.07.02 |
|---|---|
| 데이터 분석[R] - 5차시 (0) | 2021.07.01 |
| 데이터분석[R] - 4차시 (0) | 2021.06.30 |
| 데이터분석 [R] - 2차시 (0) | 2021.06.28 |
| 데이터 분석 [R] - 1차시 (0) | 2021.06.25 |



