본 글은 모두를 위한 R 데이터 분석 입문 책을 공부하면서 정리·요약한 내용입니다.
저자 : 오세종
출판 : 한빛아카데미
1. - 2 -
2. dodge
3. - 3 -
복습
1. 데이터 시각화
데이터 시각화(data visualization) : 숫자 형태의 데이터를 그래프나 그림 등의 형태로 표현하는 과정
2. 트리맵
사각타일의 형태로 구성되어 있으며, 각 타일의 크기와 색깔로 데이터의 크기를 나타냄
treemap(dtf, index, vSize, vColor = NULL, type = "index", title = NA)
3. 버블 차트
버블 차트(bubble chart): 산점도 위에 버블의 크기로 정보를 표시하는 시각화 방법
symbols(x, y)
4. 모자이크 차트
다중변수 범주형 데이터에 대해 각 변수의 그룹별 비율을 면적으로 표시하여 정보를 전달
mosaicplot(x, ...)
선그래프의 작성
날짜나 연도의 흐름에 따라서 어떻게 변하는지 정리된 데이터(시계열 자료)는 선그래프로 작성하면 보기 쉬움
airmiles

# Time Series : 시계열 데이터라는 의미
library(ggplot2)
year <- 1937:1960
cnt <- as.vector(airmiles) # 벡터로 변환 후 cnt에 저장
df <- data.frame(year, cnt) # 데이터 준비
head(df)

ggplot(data=df, aes(x=year, y=cnt))+ # 선 그래프 작성
geom_line(col="red")

연습문제
1) R에서 제공하는 mtcars 데이터셋에서 mpg(연비)에 대해 구간 간격이 5.0인 히스토그램을 ggplot으로 작성하시오.
ggplot(mtcars, aes(x=mpg))+
geom_histogram(binwidth=5.0)

2) R에서 제공하는 mtcars 데이터셋에서 mpg(연비)에 대해 ggplot으로 상자그림을 작성하되, cyl(실린더 수)에 따라 그룹을 나누어 작성하시오.
ggplot(mtcars, aes(y=mpg, fill=factor(cyl)))+
geom_boxplot()

3) 다음은 2015년부터 2026년도까지의 예상 인구수 추계 자료이다. 연도를 x축으로 하여 ggplot으로 선그래프를 작성하시오.
year <- 2015:2026
s_num <- c(51014, 51245, 51446, 51635, 51811, 51973, 52123, 52261, 52388, 52504, 52609, 52704)
d <- data.frame(year, s_num)
ggplot(data=d, aes(x=year, y=s_num))+
geom_line(col="blue")

gapminder 라이브러리
- 세계 각국의 기대 수명(lifeExp), 1인당 국내총생산(gdpPercap), 인구(pop) 데이터 등을 집계해 놓은 gapminder 데이터 셋의 일부를 담고 있음
- 5개 대륙, 총 142개 국가에 대한 1952년~2007년의 데이터가 5년간격으로 담고 있음
install.packages("gapminder")
install.packages("dplyr")
library(gapminder)
library(dplyr)
str(gapminder)
head(gapminder)
시각화를 통한 데이터 탐색
# 인구분포 순위
gapminder%>%filter(year==1952 & continent=="Asia")%>% # 끊고 결과 확인, %>%는 파이프를 의미
ggplot(aes(country, pop))+
geom_bar(stat="identity")+ # 끊고 결과 확인
coord_flip() # 끊고 결과 확인

# 인구분포 순위(로그 스케일 축)
gapminder%>%filter(year==1952 & continent=="Asia")%>% # filter는 subset과 동일한 역할을 함
ggplot(aes(reorder(country, pop), pop))+ # 크기순으로 정렬
geom_bar(stat="identity")+
scale_y_log10()+ # 큰 값은 작게, 작은 값은 크게 변환되므로 전체적인 비교가 가능
coord_flip()

# 기대수명 분포
gapminder%>%filter(year==1952)%>%
ggplot(aes(lifeExp))+ geom_histogram()

# 대륙별 기대수명 분포
gapminder%>%filter(year==1952)%>%
ggplot(aes(continent, lifeExp))+ geom_boxplot()

분석 결과
기대수명이 가장 낮은 대륙은? Africa
기대수명이 가장 높은 대륙은? Europe
아시아 기대수명 중간값은? 45
Oceania 대륙만 상자그림으로 나타내시오.
gapminder%>%filter(year==1952 & continent=="Oceania")%>%
ggplot(aes(continent, lifeExp))+ geom_boxplot()

# gdpPercap과 lifeExp의 상관관계
gapminder%>%ggplot(aes(gdpPercap, lifeExp, col=continent))+
geom_point()+scale_x_log10()

# 관측 연도를 구분
gapminder%>%ggplot(aes(gdpPercap, lifeExp, col=continent, size=pop))+
geom_point(alpha=0.2)+
facet_wrap(~year)+scale_x_log10() # facet_wrap(~year) : 연도에 따라 서브그래프를 작성

# 1952년 gdpPercap이 매우 높은 아시아 국가 찾기
gapminder%>%filter(year==1952 & gdpPercap > 10000 & continent == "Asia")

# gdpPercap의 변화(Kuwait)
gapminder%>%filter(country=="Kuwait")%>%
ggplot(aes(year, gdpPercap))+ geom_point()+ geom_line()

# pop의 변화(Kuwait)
gapminder%>%filter(country=="Kuwait")%>%
ggplot(aes(year, pop))+ geom_point()+ geom_line()

# 한국의 gdpPercap과 pop
gapminder%>%filter(country=="Korea, Rep.")%>%
ggplot(aes(year, gdpPercap))+ geom_point()+ geom_line()

gapminder%>%filter(country=="Korea, Rep.")%>%
ggplot(aes(year, pop))+ geom_point()+ geom_line()

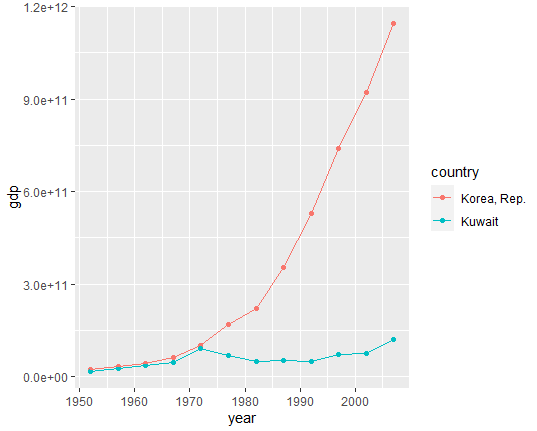
# 한국과 쿠웨이트 비교
gapminder%>%filter(country=="Kuwait" | country=="Korea, Rep.")%>%
mutate(gdp=gdpPercap*pop)%>% # mutate : 새로운 열을 하나 만들어냄
ggplot(aes(year, gdp, col=country))+ geom_point()+ geom_line()
회귀분석이란 ?
- 회귀분석(regression analysis) : 하나나 그 이상의 독립변수들이 종속변수에 미치는 영향을 추정하는 통계기법
- 변수들 사이의 인과관계를 밝히고 모형을 적합하여 관심있는 변수를 예측하거나 추론하기 위한 분석방법
- 독립변수가 하나이면 단순선형 회귀분석, 독립변수가 두 개 이상이면 다중선형 회귀분석으로 분석
기온이 증가할 때 아이스크림 판매량이 증가한다고 했을 때
기온은 원인, 아이스크림은 결과
기온은 독립변수, 아이스크림은 종속변수
회귀분석 관련 용어
영향을 주는 변수 : 독립변수(independent variable), 설명변수(explanatoryvariable)
예) 주식시세에 영향을 미치는 요인들(기업의 매출액, 원유가격, 국제정세, 정부정책 발표)
영향을 받는 변수 : 종속변수(dependent variable), 반응변수(responsevariable)
예) 독립변수의 영향에 따라 값이 결정되는 주식시세
예측모델(prediction model) 또는 예측모형 : 독립변수에 해당하는 자료와 종속변수에 해당하는 자료를 모아 관계를 분석하고 이를 예측에 사용할 수 있는 통계적 방법으로 정리한 것
단순선형 회귀분석의 목표
- 단순선형 회귀: 독립변수(x)와 종속변수(y) 사이의 선형관계를 파악하고 이를 예측에 활용하는 통계적 방법
ex) 기온(x) 자료를 가지고 아이스크림 판매량(y)을 예측하는 문제
- 단순선형 회귀모델 또는 단순선형 회귀식은 다음과 같이 1차식의 형태를 가짐
y = β0 +β1x (β0, β1 은 상수) β0는 절편, β1는 기울기
에어컨 예약대수(x)와 판매대수(y)를 이용한 회귀분석
x <- c(19, 23, 26, 29, 30, 38, 39, 46, 49) # 독립변수
y <- c(33, 51, 40, 49, 50, 69, 70, 64, 89) # 종속변수
lm(y~x) # linearmodel, y~x 순서 중요(바뀌면 안됨)

# Intercept : 절편, x : 기울기
# 식 유도 -> y = 6.409 + 1.529*x
summary(lm(y~x))

① 독립변수 : 예약대수
② 종속변수 : 판매대수
③ 회귀식 : 판매대수=6.409+1.529*예약대수
④ 귀무가설 : β1=0(종속변수는 독립변수와 인과관계가 없음)
⑤ 대립가설 : β1≠0(종속변수는 독립변수와 인과관계가 있음)
⑥ 회귀계수 β1 의 p값은 0.000581로서 0.05보다 작으므로 회귀계수가 유의미함 -> 귀무가설 기각, 대립가설 채택
⑦ 결정계수와 수정된 결정계수 모두 0.8341, 0.8104로서 데이터 설명력이 높음
주행속도와 제동거리 사이의 회귀모델 구하기
# 단순선형 회귀식을 구하기 위해서는 이론적인 이해가 필요하지만, R에서 제공하는 lm() 함수를 이용하여 쉽게 회귀식을 구할수 있음
# 독립변수는 주행속도이고 종속변수는 제동거리
head(cars)
plot(dist~speed, data=cars) # 산점도를 통해 선형 관계 확인

model <- lm(dist~speed, cars) # 회귀모델 구하기
model # 절편 : -17.579, 기울기 : 3.932

summary(model)

회귀분석 결과 :
①독립변수 : 주행속도
②종속변수 : 제동거리
③회귀식 : 제동거리 = -17.579 + 3.932*주행속도
④ 귀무가설 : β1=0(종속변수는 독립변수와 인과관계가 없음)
⑤ 대립가설 : β1≠0(종속변수는 독립변수와 인과관계가 있음)
⑥회귀계수 β1의 p값은 149e-12로서 0.05보다 작으므로 회귀계수가 유의미함
⑦ 결정계수와 수정된 결정계수 모두 0.6511, 0.6438로서데이터 설명력이 높음
abline(model) # 회귀선을 산점도 위에 표시

coef(model)[1] # b값 출력(절편) -17.57909
coef(model)[2] # W값 출력(기울기) 3.932409
주행속도에 따른 제동거리 구하기
# 주행속도가 30, 35, 40,일 때 예상 제동거리를 구함
b <- coef(model)[1]
W <- coef(model)[2]
speed <- 30 # 주행속도
dist <- W*speed+b
dist # 제동거리 (100.3932)
speed <- 35 # 주행속도
dist <- W*speed+b
dist # 제동거리 (120.0552)
speed <- 40 # 주행속도
dist <- W*speed+b
dist # 제동거리 (139.7173)
# 한번에 계산하고 출력하기
predict(model, newdata = data.frame(speed=c(30,35,40)))

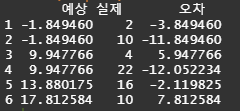
예상 제동거리, 실제 제동거리, 오차 구하기
# cars 데이터셋의 주행속도(speed) 데이터를 앞에서 구한 회귀식에 대입
speed <- cars[,1] # 주행속도
pred <- W * speed + b
pred # 예상 제동거리

compare <- data.frame(pred, cars[,2], pred-cars[,2])
colnames(compare) <- c('예상','실제','오차')
head(compare)
연습문제
1. state.x77 데이터셋에서 문맹률(Illiteracy)을 이용해 범죄율(Murder)을 예측하는 단순선형 회귀모델을 만드시오. 그리고 문맹률이 0.5, 1.0, 1.5일 때 범죄율을 예측하여 보시오.
st <- data.frame(state.x77)
model <- lm(Murder~Illiteracy, st)
model # 절편 : 2.397, 기울기 : 4.257
summary(model)
predict(model, newdata=data.frame(Illiteracy=c(0.5, 1.0, 1.5)))
2. trees 데이터셋에서 나무둘레(Girth)로 나무의 볼륨(Volume)을 예측하는 단순선형 회귀모델을 만드시오. 그리고 나무 둘레가 8.5, 9.0, 9.5일 때, 나무의 볼륨(Volume)을 예측하여 보시오.
mod <- lm(Volume~Girth, trees)
summary(mod)
# 회귀모델
# Volume = 5.0659 * Girth - 36.9435
# 볼륨예측
predict(mod, newdata=data.frame(Girth=c(8.5, 9.0, 9.5)))
'데이터 분석 > R' 카테고리의 다른 글
| 데이터 분석[R] - 11차시 (0) | 2021.07.09 |
|---|---|
| 데이터 분석[R] - 10차시 (0) | 2021.07.08 |
| 데이터 분석[R] - 8차시 (0) | 2021.07.06 |
| 데이터 분석[R] - 7차시 (0) | 2021.07.05 |
| 데이터 분석[R] - 6차시 (0) | 2021.07.02 |



